Tópico 14 – Distribuições e Amostragem
Os conceitos de “distribuição de probabilidade” e “distribuição empírica” são conceitos-chave na quantificação e no entendimento da incerteza nos dados. Nessa aula, vamos aprender a terminologia básica necessária e como incluir a incerteza do processo de amostragem nos nossos resultados.
Resultados Esperados
- Entender o que são distribuições de probabilidade e distribuições empíricas.
- Entender a diferença entre populações e amostras.
- Definir e caracterizar o que são parâmetros e o que são estatísticas.
Material Adaptado do DSC10 (UCSD)
#In:
# Imports for this lesson.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('ggplot')
# Imports for animation.
from aux14 import sampling_animation
from IPython.display import display, HTML
Distribuições de probabilidade vs. distribuições empíricas
Distribuições de probabilidade
- Considere uma variável aleatória tomando diferentes valores, cada um com uma probabilidade diferente.
- Uma variável aleatória (v.a.) é um característico numérico de um experimento aleatório, i.e. que associa valores numéricos a diferentes elementos do espaço amostral.
- Por exemplo, no lançamento de uma moeda, o espaço amostral é ${H, T}$. Podemos definir então uma v.a. $X \in {0, 1}$, onde $X = 0$ se a moeda for cara ($H$) e $X = 1$ se a moeda for coroa. Como $P(H) = P(T) = 1/2$, temos também $P(X = 0) = P(X = 1) = 1/2$.
- Uma distribuição de probabilidade descreve:
- Todos os possíveis valores da variável aleatória;
- A probabilidade teórica de cada um desses valores.
Exemplo: Distribuição de probabilidade do lançamento de um dado 🎲
A distribuição nesse caso é uniforme, isto é, cada face do dado têm a mesma probabilidade de ocorrência.
#In:
die_faces = np.arange(1, 7, 1)
die = pd.DataFrame().assign(face=die_faces)
die
| face | |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
#In:
bins = np.arange(0.5, 6.6, 1)
# Note that you can add titles to your visualizations, like this!
die.plot(kind='hist', y='face', bins=bins, density=True, ec='w',
title='Distribuição de probabilidade do lançamento de um dado',
figsize=(5, 3))
# You can also set the y-axis label with plt.ylabel.
plt.ylabel('Probabilidade');

Distribuições empíricas
Ao contrário das distribuições de probabilidade, que por definição são teóricas, as distribuições empíricas são baseadas em observações dos dados.
Usualmente, essas observações são feitas através de sucessivas repetições de um experimento.
- Uma distribuição empírica descreve:
- Todos os valores observados.
- A proporção dos experimentos em que cada valor ocorreu.
- Diferentemente das distribuições de probabilidade, as distribuições empíricas representam o que realmente ocorreu na prática.
Exemplo: Distribuição empírica do lançamento de um dado 🎲
- Vamos simular o lançamento de um dado utilizando a função
np.random.choice. - Para simular o lançamento de um dado, precisamos amostrar com reposição.
- Definiremos “reposição” mais adiante, mas aqui isso significa que se If we roll a 4, we can roll a 4 again.
#In:
num_rolls = 25
many_rolls = np.random.choice(die_faces, num_rolls)
many_rolls
array([5, 6, 1, 3, 5, 3, 4, 3, 1, 4, 5, 6, 5, 4, 6, 5, 3, 4, 5, 5, 5, 1,
5, 6, 6])
#In:
(pd.DataFrame()
.assign(face=many_rolls)
.plot(kind='hist', y='face', bins=bins, density=True, ec='w',
title=f'Distribuição empírica de {num_rolls} lançamentos de um dado',
figsize=(5, 3))
)
plt.ylabel('Frequência');

Muitos lançamentos de um dado 🎲
O que acontece quando aumentamos o número de lançamentos?
#In:
for num_rolls in [10, 50, 100, 500, 1000, 5000, 10000]:
# Don't worry about how .sample works just yet – we'll cover it shortly.
(die.sample(n=num_rolls, replace=True)
.plot(kind='hist', y='face', bins=bins, density=True, ec='w',
title=f'Distribuição de {num_rolls} lançamentos de um dado',
figsize=(8, 3))
)
plt.ylabel('Frequência')







… e porque isso acontece? ⚖️
A Lei dos Grandes Números diz que se um experimento aleatório for repetido
- um grande número de vezes,
- independentemente,
- e sobre as mesmas condições,
que então a proporção do número de vezes que um evento ocorre se aproxima cada vez mais da probabilidade teórica desse evento.
Por exemplo, à medida que lançamos um dado repetidas vezes, a proporção de vezes que obtemos um “5” chega cada vez mais perto de $\frac{1}{6}$.
A Lei dos Grandes Números garante que o uso de simulações para aproximar distribuições de probabilidade esteja correto!
Amostragem
Populações e amostras
Uma população é um grupo completo de pessoas, objetos, eventos, etc. sobre o qual queremos aprender algo.
Na prática, frequentemente não é possível obter informações sobre todos os membros de uma população.
Nessas situações, tipicamente coletamos uma amostra, isto é, um subconjunto da população.
Com base na amostra coletada, podemos estimar alguma quantidade de interesse da população.
Estratégias de amostragem
Problema principal: Como coletar uma “boa amostra”, isto é tal que a distribuição amostral seja mais parecida possível com a distribuição populacional?
- Má ideia ❌: Amostrar os indivíduos mais “próximos”/”fáceis”
- Por exemplo, seus colegas de classe, as pessoas em uma fila de supermercado, etc.
- Esse tipo de amostra é conhecido como amostra de conveniência.
- Amostras de conveniência usualmente contém fontes ocultas de viés.
- Boa ideia ✔️: Selecionar indivíduos da população de maneira aleatória.
Amostragem aleatória simples
Uma amostra aleatória simples é uma amostra coletada de maneira uniforme, aleatória e sem reposição.
- “Uniforme” significa que cada indivíduo têm a mesma probabilidade de ser selecionado.
- “Sem reposição” significa que o mesmo indivíduo não pode ser selecionado mais de uma vez.
Amostragem de uma lista ou array
Para gerar uma amostra aleatória simples de uma lista ou array options, utilizamos a função np.random.choice(options, n, replace=False).
#In:
colleges = np.array(['UFMG', 'USP', 'UEMG',
'UNICAMP', 'UFRJ', 'UFPB',
'UFSCar', 'UFSC', 'UFRGS'])
# Simple random sample of 3 colleges.
np.random.choice(colleges, 3, replace=False)
array(['USP', 'UFSCar', 'UFRJ'], dtype='<U7')
Se declararmos replace=True, então estamos amostrando uniformemente com reposição.
Exemplo: Distribuição dos atrasos de vôos ✈️
Para esse exemplo, o DataFrame united_full contém informação sobre todos os vôos da United Airlines saindo de SFO entre 6/1/15 and 8/31/15.
No contexto dessa aula, assuma que essa base de dados seja nossa população.
#In:
united_full = pd.read_csv('https://raw.githubusercontent.com/flaviovdf/fcd/master/assets/14-Amostragem/data/united_summer2015.csv')
united_full
| Date | Flight Number | Destination | Delay | |
|---|---|---|---|---|
| 0 | 6/1/15 | 73 | HNL | 257 |
| 1 | 6/1/15 | 217 | EWR | 28 |
| 2 | 6/1/15 | 237 | STL | -3 |
| 3 | 6/1/15 | 250 | SAN | 0 |
| 4 | 6/1/15 | 267 | PHL | 64 |
| ... | ... | ... | ... | ... |
| 13820 | 8/31/15 | 1978 | LAS | -4 |
| 13821 | 8/31/15 | 1993 | IAD | 8 |
| 13822 | 8/31/15 | 1994 | ORD | 3 |
| 13823 | 8/31/15 | 2000 | PHX | -1 |
| 13824 | 8/31/15 | 2013 | EWR | -2 |
13825 rows × 4 columns
Amostralindo linhas de um DataFrame
Se quisermos amostrar linhas de um DataFrame, podemos usar o método .sample. Isto é,
df.sample(n)
retorna um subconjunto aleatório de n linhas de df, amostradas sem reposição (i.e. o default dessa função é replace=False, diferente de np.random.choice).
#In:
# 5 flights, chosen randomly without replacement.
united_full.sample(5)
| Date | Flight Number | Destination | Delay | |
|---|---|---|---|---|
| 6610 | 7/15/15 | 663 | HNL | 6 |
| 1704 | 6/12/15 | 704 | JFK | 159 |
| 13118 | 8/27/15 | 205 | PDX | -9 |
| 10544 | 8/9/15 | 1774 | IAD | -1 |
| 11794 | 8/17/15 | 1734 | BOS | 2 |
#In:
# 5 flights, chosen randomly with replacement.
united_full.sample(5, replace=True)
| Date | Flight Number | Destination | Delay | |
|---|---|---|---|---|
| 4288 | 6/29/15 | 1247 | SAN | 4 |
| 11471 | 8/15/15 | 1662 | ORD | 4 |
| 11244 | 8/14/15 | 486 | IAD | -2 |
| 373 | 6/3/15 | 1135 | RDU | -7 |
| 428 | 6/3/15 | 1711 | IAH | 6 |
Nota: A probabilidade de observarmos a mesma linha mais de uma vez ao reamostrarmos com reposição nesse caso é baixa, uma vez que aqui o tamanho amostral (5) é pequeno relativo ao tamanho da população (13825).
O efeito do tamanho amostral
A Lei dos Grandes Números diz que, à medida que aumentamos o número de repetições de um experimento aleatório, a distribuição empírica se aproxima cada vez mais da distribuição de probabilidade verdadeira (populacional).
Como consequência, em um processo de amostragem aleatória simples, quanto maior o nosso tamanho amostral, melhor será nossa aproximação da distribuição de probabilidade populacional.
- Tecnicalidades à parte, uma maneira intuitiva de entender esse ponto é enxergar que, como as amostras aleatórias simples são independentes e vêm da mesma população, uma amostra grande pode ser sempre decomposta em várias amostras pequenas.
Distribuição populacional dos atrasos de vôos ✈️
Aqui estamos interessados apenas nos 'Delay's, então selecionaremos apenas essa coluna.
#In:
united = united_full.get(['Delay'])
united
| Delay | |
|---|---|
| 0 | 257 |
| 1 | 28 |
| 2 | -3 |
| 3 | 0 |
| 4 | 64 |
| ... | ... |
| 13820 | -4 |
| 13821 | 8 |
| 13822 | 3 |
| 13823 | -1 |
| 13824 | -2 |
13825 rows × 1 columns
#In:
bins = np.arange(-20, 300, 10)
united.plot(kind='hist', y='Delay', bins=bins, density=True, ec='w',
title='Distribuição Populacional dos Atrasos de Vôos', figsize=(8, 3))
plt.ylabel('Proporção por minuto');

Note que a distribuição populacional é “determinística” (ou “fixa”), isto é, supondo que o universo de todos os possíveis valores que estamos interessados seja conhecido, não existe aleatoriedade como em um processo de amostragem.
Distribuição amostral dos atrasos de vôos ✈️
- Aqui, nossa população é composta dos 13825 atrasos de vôos no DataFrame
united. - Em geral, porém, raramente temos acesso à população inteira.
- Para replicar uma situação prática real, vamos reamostrar de
unitedsem reposição.
#In:
sample_size = 100 # Change this and see what happens!
(united
.sample(sample_size)
.plot(kind='hist', y='Delay', bins=bins, density=True, ec='w',
title=f'Distribuição dos Atrasos de Vôos em uma Amostra de Tamanho $n = {sample_size}$',
figsize=(8, 3))
)
plt.ylabel('Frequência');

Note que, intuitivamente, à medida que aumentos o tamanho amostral $n$ (sample_size), a distribuição amostral dos atrasos fica cada vez mais parecida com a distribuição populacional.
Parâmetros e estatísticas
Definições
Inferência estatística é o ato de se tirar conclusões sobre uma população com base nas informações de uma amostra aleatória.
- Parâmetro: Uma quantidade de interesse da população.
- Exemplo 1: A média populacional.
- Exemplo 2: A proporção populacional.
- Estatística: Uma quantidade calculada com base na amostra.
- Exemplo 1: A média amostral.
- Exemplo 2: A proporção amostral.
- Uma estatística pode ser utilizada para estimar um parâmetro.
- Como uma função matemática teórica, diz-se que uma estatística nesse caso é um estimador para esse parâmetro.
- Após coletarmos uma amostra, o valor correspondete que a estatística/estimador toma é então uma estimativa para o parâmetro.
Média de atrasos dos vôos ✈️
Pergunta: Qual foi a média de atraso entre todos os vôos da United saindo de SFO no verão de 2015? 🤔
Em geral, gostaríamos de saber a média dos atrasos de vôos na população (nosso parâmetro), mas na prática teremos disponível apenas uma amostra.
É natural então perguntarmos: como a média dos atrasos dos vôos na amostra (isto é, a estatística) se compara à média dos atrasos dos vôos na população (nosso parâmetro)?
Média populacional
A média populacional é um parâmetro.
#In:
# Calculate the mean of the population.
united_mean = united.get('Delay').mean()
united_mean
16.658155515370705
A média populacional (assim como a distribuição populacional) também é determinística, ou fixa (i.e. não aleatória), assim como qualquer outro parâmetro. Como quase nunca temos acesso à população completa, em geral não podemos saber com exatidão os valores dos parâmetros sobre os quais estamos interessados.
Em outras palavras, embora os parâmetros sejam fixos, em geral eles também são desconhecidos.
Média amostral
A média amostral é uma estatística. Como estatísticas são funções da amostra (e que por definição é aleatória), a média amostral também é aleatória.
#In:
# Sample size = 100.
sample_size = 100
united.sample(sample_size).get('Delay').mean()
13.06
- Cada vez que executamos a célula acima, nós estamos:
- Coletando uma nova amostra aleatória de tamanho $n$ =
sample_size. - Calculando a média amostral correspondente.
- Coletando uma nova amostra aleatória de tamanho $n$ =
- Note que, a cada execução, a média amostral é ligeiramente diferente.
- Algumas vezes, a média amostral é próxima da média populacional.
- Algumas vezes, a média amostral é distante da média populacional.
O efeito do tamanho amostral
E se coletarmos um tamanho de amostra maior?
#In:
# Sample size = 1000
sample_size = 1000
united.sample(sample_size).get('Delay').mean()
15.052
- Cada vez que executamos a célula acima, os resultados ainda são ligeiramente diferentes.
- Entretanto, se compararmos à situação anterior em que $n = 100$, as médias amostrais agora são muito mais próximas entre si – e também mais próximas à média populacional.
- Em geral, estatísticas calculadas com base em amostras maiores são estimadores melhores dos parâmetros da população do que quando calculadas em amostras menores.
Tamanhos de amostra menores:
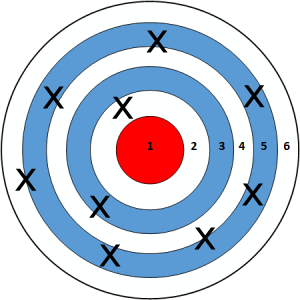
Tamanhos de amostra maiores:
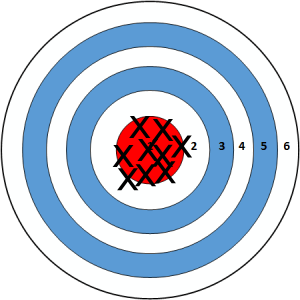
Distribuição de probabilidade de uma estatística
- O valor numérico de uma estatística, (por exemplo a média amostral) é aleatório, porque é calculado com base em uma amostra (que é aleatório).
- Mais formalmente, estatísticas também são variáveis aleatórias.
- Assim como fazemos para variáveis aletaórias em geral, podemos analisar a distribuição de probabilidade da estatística na qual estamos interessados.
- Essa distribuição é conhecida como distribuição amostral.
- A distribuição amostral descreve a probabilidade de todos os possíveis valores de uma estatística.
- A distribuição amostral é útil para caracterizar o quão provável é o valor da estatística em uma amostra particular.
- De maneira análoga, a distribuição empírica nos permite dizer o quanto o valor da nossa estatística poderia ter sido caso tívessemos coletado uma amostra diferente.
- Infelizmente, porém, a distribuição empírica pode ser difícil de se caracterizar de maneira exata/analítica.
- Temos então basicamente 2 maneiras de encontramos essa distribuição:
- Opção 1: Desenvolver uma expressão geral matematicamente (nos casos em que isso é possível).
- Opção 2: Gerar todas as possíveis amostras e calcular o valor da estatística para cada amostra.
- Nesse curso, focaremos na Opção 2, isto é, utilizaremos simulação para aproximar a distribuição amostral das estatísticas nas quais estamos interessados.
- A Opção 1 será o assunto de vários dos cursos de Estatística mais adiante!
Distribuição empírica de uma estatística
- A distribuição empírica de uma estatística é obtida com base nos valores simulados de uma estatística. Essa distribuição descreve:
- Todos os valores observados da estatística.
- A frequência/proporção de amostras em que cada valor foi observado.
- Em geral, a distribuição empírica de uma estatística se torna uma aproximação cada vez melhor para a distribuição amostral daquela estatística (i.e. a verdadeira distribuição de probabilidades da estatística) à medida que o número de repetições da simulação é cada vez maior.
Distribuição das médias amostrais
- Para entendermos o quão diferente o valor da média amostral pode ser em diferentes amostras, nós faremos o seguinte:
- Geramos muitas amostras aleatoriamente;
- Calculamos a média amostral em cada uma das amostras;
- Fazemos um histograma com os valores obtidos.
- A animação abaixo contém uma visualização do seguinte processo, repetido várias vezes:
- 1.) gerar $n = 1000$ atrasos de vôos de `united’;
- 2.) calcular a média amostral correspondente;
- 3.) agregar o valor à um histograma.
#In:
%%capture
anim, anim_means = sampling_animation(united, 1000);
#In:
HTML(anim.to_jshtml())
Mas afinal, para que serve a distribuição empírica de uma estatística?
- Na prática, coletamos apenas uma amostra, da qual calculamos apenas um valor da estatística.
- Em certos casos, a amostra pode ser suficientemente representativa da população, e o valor da estatística será próximo ao parâmetro que estamos tentando estimar.
- Quando isso não acontece, porém, i.e. quando a amostra não é tão representativa da população, o valor da estatística pode ser bem diferente do parâmetro de interesse.
- Dessa forma, a distribuição empírica de uma estatística nos ajuda a responder à seguinte pergunta: qual seria o valor da estatística caso tívessemos coletado uma amostra diferente?
E qual o papel do tamanho amostral nesse processo?
#In:
# Sample one thousand flights, two thousand times.
sample_size = 1000
repetitions = 2000
sample_means = np.array([])
for n in np.arange(repetitions):
m = united.sample(sample_size).get('Delay').mean()
sample_means = np.append(sample_means, m)
pd.DataFrame().assign(sample_means=sample_means) \
.plot(kind='hist', bins=np.arange(10, 25, 0.5), density=True, ec='w',
title=f'Distribuição da Média Amostral com $n = {sample_size}$',
figsize=(10, 5));
plt.axvline(x=united_mean, c='black', linewidth=4, label='média populacional')
plt.legend()
plt.ylabel('Frequência');

Teste Rápido ✅
No exemplo acima, amostramos amostras de vôos de tamanho $n = 1000$ um número $B = 2000 de vezes. Se ao invés disso continuarmos amostrando $B = 2000 vezes, mas agora amostras de tamanho $n = 100$, qual você acha que será o efeito sobre a distribuição empírica da média amostral?
- A. Ficará mais estreita
- B. Ficará mais larga
- C. Será deslocada para a esquerda
- D. Será deslocada para a direita
- E. Nenhum
A maneira como amostramos importa!
- Até agora, assumimos que estamos coletando apenas amostras aleatórias simples da população de interesse.
- Recorde que amostras aleatórias simples são tomadas sem reposição.
- Entretanto, se a população for grande o suficiente (possivelmente infinita…), amostragens sem e com reposição serão equivalentes.
A média amostral, sob amostragem aleatória simples, é uma boa aproximação para a média populacional.
- Mas isso nem sempre é verdade se amostrarmos de maneira diferente!
- Voltaremos à esse ponto depois, mas uma situação importante onde isso pode acontecer é quando o processo de amostragem é enviesado (você consegue pensar em um exemplo simples disso?).
Resumo e próxima aula
Resumo
- A distribuição de probabilidade de uma variável aleatória descreve a probabilidade de cada possível valor dessa variável.
- Uma distribuição empírica descreve a frequência/proporção com a qual cada valor de um experimento aleatório ocorre.
- Quanto mais repetimos o experimento aleatório, mais a distribuição empírica se aproxima da distribuição de probabilidade.
- A distribuição populacional descreve as probabilidades associadas aos valores de uma certa característica de interesse de uma população.
- Uma distribuição amostral descreve as probabilidades associadas aos valores de uma certa característica da amostra, que é um subconjunto da população.
- Quando coletamos uma amostra aleatória simples da população, à medida que o tamanho amostral $n$ aumenta, mais a distribuição amostral se aproxima da distribuição populacional.
- Um parâmetro é uma quantidade de interesse da população, enquanto uma estatística é uma quantidade de interesse da amostra.
- Em geral, podemos utilizar estatísticas para estimar parâmetros da população.
- Por exemplo, para estimar a média populacional, podemos utilizar a média amostral.
- Usualmente, amostras de tamanhos maiores levam à estimativas mais precisas.
Próxima aula
- Maiores tamanhos de amostra levam à estimativas mais precisas, mas como balancear essa precisão com o custo e outros desafios de ordem prática na hora de coletar amostras “grandes”?
- Introduziremos nesse contexto uma solução criativa denominada bootstrapping 🥾, que nos permite ter alguns dos benefícios de uma amostra maior do que a coletada para melhorar nossas estimativas!