Tópico 18 – O Teorema Central do Limite
Na sequência do que aprendemos sobre a distribuição Normal, vamos ver nessa aula um resultado impressionante que motiva o uso dessa distribuição na grande maioria das aplicações em Ciência de Dados: O Teorema Central do Limite. Em linhas gerais, esse resultado diz que, ainda que a distribuição populacional na qual estamos interessados não seja aproximadamente Normal, a distribuição da média de uma amostra tomada dessa distribuição vai ser, sob condições muito razoáveis, aproximadamente Normal. Além disso, o resultado corrobora nossa intuição de que, quanto maior o tamanho da amostra sob a qual a média amostral é calculada, mais precisa é nossa estimativa e melhor é a aproximação resultante.
Resultados Esperados
- Introduzir o Teorema Central do Limite (TCL).
- Aprender a utilizar o TCL para fazer Inferência, em particular para calcular probabilidades e construir intervalos de confiança.
- Discutir a influência do tamanho amostral em nossas estimativas, e comparar os prós e contras de se utilizar o bootstrap e o TCL nesse contexto.
Material Adaptado do DSC10 (UCSD)
#In:
import numpy as np
import pandas as pd
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from scipy import stats
np.set_printoptions(threshold=20, precision=2, suppress=True)
pd.set_option("display.max_rows", 7)
pd.set_option("display.max_columns", 8)
pd.set_option("display.precision", 2)
# Animations
import time
from IPython.display import display, HTML, IFrame, clear_output
import ipywidgets as widgets
import warnings
warnings.filterwarnings('ignore')
def normal_curve(x, mu=0, sigma=1):
return (1 / np.sqrt(2 * np.pi * sigma ** 2)) * np.exp((- (x - mu) ** 2) / (2 * sigma ** 2))
def normal_area(a, b, bars=False, title=None):
x = np.linspace(-4, 4)
y = normal_curve(x)
ix = (x >= a) & (x <= b)
plt.plot(x, y, color='black')
plt.fill_between(x[ix], y[ix], color='gold')
if bars:
plt.axvline(a, color='red')
plt.axvline(b, color='red')
if title:
plt.title(title)
else:
plt.title(f'Area between {np.round(a, 2)} and {np.round(b, 2)}')
plt.show()
def area_within(z):
title = f'Proportion of values within {z} SDs of the mean: {np.round(stats.norm.cdf(z) - stats.norm.cdf(-z), 4)}'
normal_area(-z, z, title=title)
def show_clt_slides():
src = "https://docs.google.com/presentation/d/e/2PACX-1vTcJd3U1H1KoXqBFcWGKFUPjZbeW4oiNZZLCFY8jqvSDsl4L1rRTg7980nPs1TGCAecYKUZxH5MZIBh/embed?start=false&loop=false&delayms=3000&rm=minimal"
width = 960
height = 509
display(IFrame(src, width, height))
def estimate_z():
z = widgets.FloatSlider(value=2, min=0,max=4,step=0.05, description='z')
ui = widgets.HBox([z])
out = widgets.interactive_output(area_within, {'z': z})
display(ui, out)
def plot_many_distributions(sample_sizes, sample_means):
bins = np.arange(5, 30, 0.5)
for size in sample_sizes:
pd.DataFrame().assign(data=sample_means[size]).plot(kind='hist', bins=bins, density=True, ec='w', title=f'Distribution of the Sample Mean for Samples of Size {size}', figsize=(8, 4))
plt.legend('');
plt.show()
time.sleep(1.5)
if size != sample_sizes[-1]:
clear_output()
Recapitulando: Padronização
Unidades padronizadas
Lembre que, se $X$ é uma variável aleatória (numérica) com média $\mu$ e variância $\sigma^2$, e se $X_i$ é um valor (realização) dessa variável, então
\[\begin{align*} Z_i := \frac{X_i - \mu}{\sigma} \end{align*}\]representa $X_i$ em unidades padronizadas, isto é, o número de DPs $\sigma$ que $X_i$ está de sua média $\mu$ .
Na versão amostral, isto é, após coletar uma amostra $\mathbf{X} := (X_1, \ldots, X_n)$ com média $\bar{X}$ e variância $S^2$, as observações padronizadas são definidas por
\begin{align} Z_i := \frac{X_i - \bar{X}}{S}, \end{align}
com a mesma interpretação acima, mas relativa à distribuição da amostra.
Exemplo rápido: pontuação no SAT
As notas no SAT vão de 0 a 1,600. A distribuição das notas do SAT tem uma média de 950 e um desvio padrão de 300.
Se um amigo te diz que ele tirou 2.5 no SAT (em unidades padronizadas), o que você conclui?
O Teorema Central do Limite
Atrasos de vôos (mais uma vez) ✈️
A distribuição dos atrasos de vôos que analisamos anteriormente não é aproximadamente Normal.
#In:
delays = pd.read_csv('https://raw.githubusercontent.com/flaviovdf/fcd/master/assets/17-Normalidade/data/united_summer2015.csv')
delays.plot(kind='hist', y='Delay', bins=np.arange(-20.5, 210, 5), density=True, ec='w', figsize=(10, 5), title='Distribuição Populacional dos Atrasos de Vôos')
plt.xlabel('Atrasos (em minutos)')
plt.ylabel("Frequência");

#In:
delays.get('Delay').describe()
count 13825.00
mean 16.66
std 39.48
...
50% 2.00
75% 18.00
max 580.00
Name: Delay, Length: 8, dtype: float64
Distribuição empírica de uma estatística
Antes de apresentarmos as medidas de centralidade, dispersão e a distribuição Normal, discutimos o bootstrap.
Mais especificamente, utilizamos o boostrap para construir uma aproximação para a distribuição de uma estatística (por exemplo a média ou a mediana amostrais), com base em uma única amostra.
A partir dessa distribuição (a distribuição bootstrap da estatística), construímos intervalos de confiança para o parâmetro populacional de interesse.
- No contexto dessa aula, suponha que nosso parâmetro de interesse seja a média populacional.
- Estaremos então interessados em aproximar a distribuição da média amostral.
- Nessa aula, introduziremos uma técnica para aproximar a distribuição da média amostral sem recorrermos ao bootstrap.
- Faremos isso com a utilização do ferramental de Inferência Estatística, desenvolvida com sólidos fundamentos matemáticos baseados na Teoria de Probabilidade.
- Lembre da nossa discussão em sala de aula: a teoria Estatística e o ferramental matemático em geral devem fundamentar, integrar e complementar o que conseguimos aprender a calcular com base em métodos de simulação!
Distribuição empírica da média amostral
Como nesse caso específico temos acesso à população dos atrasos de vôos, inicialmente vamos aproximar a distribuição amostral da média com base na média amostral de diferentes amostras, tiradas (com reposição) da população original.
- Importante: isso não é boostrapping!
- Essa abordagem também não é muito prática.
- Se tivéssemos acesso à população completa, não precisaríamos realizar nenhum tipo de inferência – bastaria simplesmente calcular a média populacional diretamente.
#In:
sample_means = np.array([])
repetitions = 2000
for i in np.arange(repetitions):
sample = delays.sample(500) # Not bootstrapping!
sample_mean = sample.get('Delay').mean()
sample_means = np.append(sample_means, sample_mean)
sample_means
array([15.88, 15.42, 15.79, ..., 17.11, 16.93, 17.1 ])
#In:
pd.DataFrame().assign(sample_means=sample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.scatter([sample_means.mean()], [-0.005], marker='^', color='green', s=250)
plt.axvline(sample_means.mean(), color='green', label=f'mean={np.round(sample_means.mean(), 2)}', linewidth=4)
plt.xlim(5, 30)
plt.ylim(-0.013, 0.26)
plt.legend()
plt.ylabel("Frequência");

Note que essa distribuição é aproximadamente Normal, ainda que a distribuição da população não seja.
Note ainda que a distribuição empírica das médias construída dessa maneira está centrada na média populacional.
O Teorema Central do Limite
O Teorema Central do Limite (TCL) nos diz que a distribuição de probabilidade da média de uma amostra de tamanho “grande o suficiente” será “sempre” aproximadamente Normal, qualquer que seja a população da qual a amostra foi retirada.
Embora as fórmulas a seguir dizem respeito ao comportamento de médias, os resultados do teorema são válidos também para diferentes tipos de somas.
Características da distribuição da média amostral
Forma: O TCL nos diz que a distribuição da média amostral será sempre aproximadamente Normal.
Locação: A distribuição da média amostral vai estar centrada na média populacional.
Escala: Discutiremos um pouco abaixo sobre a variância/desvio padrão da distribuição da média amostral.
- Mas antes, para refletir, pense na seguinte pergunta: “Como a dispersão dessa distribuição seria afetada pelo tamanho amostral?”
Influência do tamanho amostral
A função sample_mean_delays definida abaixo toma um argumento do tipo integer (sample_size), e então:
- Toma uma amostra de tamanho $n = $
sample_sizeda população de atrasos de vôos. - Calcula a média amostral correspondente.
- Repõe a amostra e itera os passos 1 a 2 acima um número $M = 2.000$ de vezes, retornando uma array com as médias amostrais de cada iteração.
#In:
def sample_mean_delays(sample_size):
sample_means = np.array([])
for i in np.arange(2000):
sample = delays.sample(sample_size)
sample_mean = sample.get('Delay').mean()
sample_means = np.append(sample_means, sample_mean)
return sample_means
#In:
sample_size = 100
sample_mean_delays(sample_size)
array([12.93, 14.35, 7.7 , ..., 12.87, 15.69, 15.12])
Vamos agora invocar sample_mean_delays em um array contendo diferentes valores de sample_size.
#In:
sample_means = {}
sample_sizes = [5, 10, 50, 100, 200, 400, 800, 1600]
for size in sample_sizes:
sample_means[size] = sample_mean_delays(size)
sample_means
{5: array([10.8, 11. , 38. , ..., 20.6, 7.8, 15.4]),
10: array([ 2.2, 10.7, 19.2, ..., 12. , 8.8, 7.1]),
50: array([21.6 , 18.42, 17.66, ..., 11.26, 14.98, 8.34]),
100: array([20.96, 16.1 , 19.97, ..., 18.81, 11.18, 20.4 ]),
200: array([18.66, 16.21, 17.39, ..., 19.11, 16.32, 14.21]),
400: array([18.54, 17.35, 13.76, ..., 15.51, 15.56, 20.91]),
800: array([15.6 , 18.01, 17.2 , ..., 17.32, 14.28, 16.76]),
1600: array([16.62, 16.49, 16.97, ..., 17.04, 17.11, 14.73])}
Vamos agora analisar as distribuições (empíricas) das médias amostrais resultantes desse processo.
#In:
plot_many_distributions(sample_sizes, sample_means)

O que você consegue notar no processo acima? 🤔
Variância da distribuição da média amostral
- À medida que o nosso tamanho amostral $n$ aumenta, a distribuição da média se torna cada vez “mais Normal”, e sua variância diminui.
- Visualmente, utilizando o que sabemos sobre a distribuição Normal, você consegue determinar aproximadamente o quanto a variância diminui com o tamanho amostral?
#In:
# Compute the standard deviation of each distribution.
vars = np.array([])
for size in sample_sizes:
var = np.var(sample_means[size])
vars = np.append(vars, var)
vars
array([279.7 , 140. , 31.96, 15.54, 7.28, 4.14, 1.82, 0.85])
#In:
observed = pd.DataFrame().assign(
SampleSize=sample_sizes,
Variance=vars
)
observed.plot(kind='scatter', x='SampleSize', y='Variance', s=70, title="Variância da Distribuição da Média Amostral vs. Tamanho Amostral", figsize=(10, 5))
plt.xlabel("$n$")
plt.ylabel("Variância");

Aparentemente, à medida que $n$ aumenta, a variância da distribuição da média amostral diminui drasticamente.
Variância da distribuição da média amostral
- À medida que aumentamos o tamanho amostral, a distribuição da média amostral fica cada vez mais “estreita”, isto é, menos dispersa.
- Em outras palavras, a distribuição da média amostral fica cada vez mais concentrada em torno da média populacional.
- Mais precisamente, a lei que rege a variância das médias amostrais é do tipo
\begin{align} \text{var}(\bar{X}) = \frac{\sigma^2}{n}, \end{align}
em que $\sigma^2$ é a variância populacional.
- Em outras palavras, à medida que o tamanho amostral $n$ cresce, a variância das médias amostrais diminui de maneira diretamente proporcional (i.e. linear).
- Analogamente, o desvio padrão diminui com a raiz quadrada de $n$, pois aqui $\sqrt{\text{var}(\bar{X})} = \sigma/\sqrt{n}$.
Essas definições e resultados serão explicadas de maneira mais precisa em um próximo curso de Probabilidade.
No contexto desse curso, porém, temos uma conclusão importante: quando coletamos amostras de tamanho maior, a média amostral se aproxima cada vez mais da média populacional.
Isto é, à medida que o tamanho amostral aumenta, nossa estimativa para a média populacional se torna cada vez melhor!
- Importante: A afirmação acima não é sobre a variância ou desvio padrão amostrais $S^2$ e $S$, mas sim sobre a variância/DP populacional, que é relativa à distribuição de todas as possíveis médias amostrais.
- Dessa forma, ao aumentar o tamanho amostral $n$:
- Não é verdade ❌ que nosso DP amostral $S$ vai diminuir;
- É verdade ✅ que o DP da distribuição amostral da média amostral (e que é igual ao DP populacional $\sigma$ dividido por $\sqrt{n}$) vai diminuir.
Recapitulando: Distribuição da média amostral
Forma: O TCL nos diz que a distribuição da média amostral será sempre aproximadamente Normal.
Locação: A distribuição da média amostral vai estar centrada na média populacional.
Escala: A variância da distribuição da média amostral diminui linearmente com $n$ (e o desvio padrão correspondente diminui com $\sqrt{n}$).
🚨 Problema: Tanto a média quanto o desvio padrão da média amostral dependem de parâmetros da populacão original ($\mu$ e $\sigma^2$), mas na prática não temos acesso à essa informação!
Boostrap vs. TCL
Lembre que no bootstrap nosso objetivo era aproximar a distribuição de uma estatística (por exemplo, a média amostral), utilizando simulação e nos baseando em uma única amostra.
O TCL descreve o comportamento a distribuição da média amostral através de uma lei matemática/Estatística, mas depende de informação da população ($\mu$ e $\sigma$).
Ideia importante: A média $\bar{X}$ e o DP $S$ amostrais são usualmente boas aproximações para $\mu$ e $\sigma$, respectivamente. Dessa forma, podemos utilizá-los como aproximações no próprio TCL!
Dessa forma, com base no TCL podemos aproximar a distribuição da média amostral, com base em uma única amostra, mas sem bootstrap nem simulação!
Aproximando a distribuição da média amostral via bootstrap
Vamos começar tomando uma amostra de tamanho $n = 500$ do DataFrame delays.
#In:
np.random.seed(42)
my_sample = delays.sample(500)
my_sample.get('Delay').describe()
count 500.00
mean 13.01
std 28.00
...
50% 3.00
75% 16.00
max 209.00
Name: Delay, Length: 8, dtype: float64
Para aproximar a distribuição da média amostral, podemos realizar então um bootstrap (aqui $B = 2,000$):
#In:
resample_means = np.array([])
repetitions = 2000
for i in np.arange(repetitions):
resample = my_sample.sample(500, replace=True) # Bootstrapping!
resample_mean = resample.get('Delay').mean()
resample_means = np.append(resample_means, resample_mean)
resample_means
array([12.65, 11.5 , 11.34, ..., 12.59, 11.89, 12.58])
#In:
pd.DataFrame().assign(resample_means=resample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.scatter([resample_means.mean()], [-0.005], marker='^', color='green', s=250)
plt.axvline(resample_means.mean(), color='green', label=f'mean={np.round(resample_means.mean(), 2)}', linewidth=4)
plt.xlim(7, 20)
plt.ylim(-0.015, 0.35)
plt.legend()
plt.ylabel("Frequência");

Aproximando a distribuição da média amostral com o TCL
Utilizando a média amostral $\bar{X}$ e a variância amostral $S^2$ como estimativas da média populacional $\mu$ e da variância populacional $\sigma^2$, o TCL nos diz que a distribuição da média amostral será aproximadamente Normal, centrada na própria média amostral $\bar{X}$ e com variância igual a $S^2/n$.
A média amostral de my_sample é igual a:
#In:
sample_mean_mean = my_sample.get('Delay').mean()
sample_mean_mean
13.008
e o desvio padrão correspondente é:
#In:
sample_mean_sd = np.std(my_sample.get('Delay')) / np.sqrt(my_sample.shape[0])
sample_mean_sd
1.2511114546674091
Vamos então elaborar o gráfico de uma curva Normal com média $\bar{X}$ e DP $S/\sqrt{n}$ e sobrepor à distribuição bootstrap obtida acima.
#In:
norm_x = np.linspace(7, 20)
norm_y = normal_curve(norm_x, mu=sample_mean_mean, sigma=sample_mean_sd)
pd.DataFrame().assign(Bootstrapping=resample_means).plot(kind='hist', density=True, ec='w', alpha=0.65, bins=20, figsize=(10, 5));
plt.plot(norm_x, norm_y, color='black', linestyle='--', linewidth=4, label='CLT')
plt.title('Distribuição da Média Amostral, via Bootstrap e TCL')
plt.xlim(7, 20)
plt.legend()
plt.ylabel("Frequência");

A aproximação é muito boa, e sem fazer nenhuma simulação!
#In:
show_clt_slides()
Intervalos de confiança utilizando o TCL
Da mesma forma que fizemos através do bootstrap, podemos construir intervalos de confiança também com o TCL.
Lembre que, no bootstrap, os intervalos de $\gamma\%$ de confiança são em geral calculados como os percentis $(1 - \gamma)/2$ e $(1 + \gamma)/2$ da distribuição bootstrap.
Utilizando o TCL, basta pegarmos os mesmos percentis, porém da distribuição Normal com média $\bar{X}$ e variância $\sigma^2/n$.
Intervalo de 95% de confiança via bootstrap
Com base nos resultados do bootstrap acima ($B = 2,000$), os percentis 2.5% e 97.5% da distribuição bootstrap são:
#In:
left_boot = np.percentile(resample_means, 2.5)
right_boot = np.percentile(resample_means, 97.5)
[left_boot, right_boot]
[10.7159, 15.43405]
Visualmente:
#In:
pd.DataFrame().assign(resample_means=resample_means).plot(kind='hist', y='resample_means', alpha=0.65, bins=20, density=True, ec='w', figsize=(10, 5), title='Distribuição Bootstrap da Média Amostral');
plt.plot([left_boot, right_boot], [0, 0], color='gold', linewidth=10, label='95% bootstrap-based confidence interval');
plt.axvline(resample_means.mean(), color='green', label=f'sample mean={np.round(resample_means.mean(), 2)}', linewidth=4)
plt.xlim(7, 20);
plt.legend()
plt.ylabel("Frequência");

Intervalo de 95% de confiança via TCL
Com o TCL, basta tomarmos os percentis 2.5% e 97.5% da distribuição Normal com média $\bar{X}$ e variância $S^2/n$.
A média amostral aqui é igual a
#In:
sample_mean_mean = my_sample.get('Delay').mean()
sample_mean_mean
13.008
E o desvio padrão amostral (dividido pela raiz do tamanho amostral) é igual a
#In:
sample_mean_sd = np.std(my_sample.get('Delay')) / np.sqrt(my_sample.shape[0])
sample_mean_sd
1.2511114546674091
Dessa forma, a distribuição da média amostral é, aproximadamente:
#In:
plt.figure(figsize=(10, 5))
norm_x = np.linspace(7, 20)
norm_y = normal_curve(norm_x, mu=sample_mean_mean, sigma=sample_mean_sd)
plt.plot(norm_x, norm_y, color='black', linestyle='--', linewidth=4, label='Distribution of the Sample Mean (via the CLT)')
plt.xlim(7, 20)
plt.legend();

- Para encontrarmos os percentis 2.5% e 97.5% dessa distribuição, lembre da última aula que, na distribuição Normal, aproximadamente 95% dos valores estão a 2 DPs da média.
- Isso vale para qualquer distribuição Normal!
- Utilizando esse fato, como a média da distribuição acima é igual a $\bar{X}$ e seu desvio padrão é igual a $S/\sqrt{n}$, temos que o percentil 2.5% (limite inferior do IC95%) é igual a $\bar{X} - 2 \cdot S/\sqrt{n}$, e o percentil 95% (limite superior do IC95%) é igual a $\bar{X} + 2 \cdot S/\sqrt{n}$.
#In:
left_normal = sample_mean_mean - 2 * sample_mean_sd
right_normal = sample_mean_mean + 2 * sample_mean_sd
[left_normal, right_normal]
[10.50577709066518, 15.510222909334818]
Visualmente:
#In:
plt.figure(figsize=(10, 5))
norm_x = np.linspace(7, 20)
norm_y = normal_curve(norm_x, mu=sample_mean_mean, sigma=sample_mean_sd)
plt.plot(norm_x, norm_y, color='black', linestyle='--', linewidth=4, label='Distribuição da Média Amostral (via TCL)')
plt.xlim(7, 20)
plt.ylim(0, 0.41)
plt.plot([left_normal, right_normal], [0, 0], color='#8f6100', linewidth=10, label='95% CLT-based confidence interval')
plt.axvline(resample_means.mean(), color='green', label=f'sample mean={np.round(resample_means.mean(), 2)}', linewidth=4)
plt.legend();

Comparando os intervalos
Vamos agora comparar os ICs obtidos por ambas as técnicas!
O IC via bootstrap é dado por
#In:
[left_boot, right_boot]
[10.7159, 15.43405]
e o IC calculado através do TCL é dado por
#In:
[left_normal, right_normal]
[10.50577709066518, 15.510222909334818]
Os resultados são bem próximos!
Resumo: IC para a média populacional via TCL
Com base no TCL, o IC95% para a média populacional é dado por
\begin{equation} IC_{95\%}(\mu) = \bar{X} \pm 2 \cdot \frac{S}{\sqrt{n}} = \left[\bar{X} - 2 \cdot \frac{S}{\sqrt{n}}; \,\,\,\, \bar{X} + 2 \cdot \frac{S}{\sqrt{n}}\right]. \end{equation}
Analogamente, para um nível $\gamma\%$ qualquer de confiança (i.e. para $0 < \gamma < 1$), temos
\begin{equation} IC_{\gamma\%}(\mu) := \bar{X} \pm Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}} = \left[\bar{X} - Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}}; \,\,\,\, \bar{X} + Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}}\right], \end{equation}
onde $Z_{(1 + \gamma)/2}$ denota o percentil $(1 + \gamma)/2$ da distribuição Normal padrão.
Observações acerca dos percentis da distribuição Normal
Se quisermos ser mais precisos, o quantil 2.5% e 97.5% da distribuição Normal padrão são, na verdade, aproximadamente $\pm 1.96$.
#In:
normal_area(-2, 2)

#In:
stats.norm.cdf(2) - stats.norm.cdf(-2)
0.9544997361036416
#In:
normal_area(-1.96, 1.96)

#In:
stats.norm.cdf(1.96) - stats.norm.cdf(-1.96)
0.950004209703559
Porém, na maioria dos casos, tomar $\pm 2$ leva à uma aproximação bem razoável, com uma diferença de apenas $0.45\%$ na probabilidade entre $\pm 1.96$ e $\pm 2$.
Por último, note que o intervalo definido na fórmula acima é na verdade dado por
\begin{equation} \left[\bar{X} + Z_{(1 - \gamma)/2} \cdot \frac{S}{\sqrt{n}}; \,\,\,\, \bar{X} + Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}}\right]. \end{equation}
Porém, utilizando a propriedade de reflexividade da distribuição Normal, sabemos que $Z_{(1 + \gamma)/2} > 0$ e que $Z_{(1 - \gamma)/2} = - Z_{(1 + \gamma)/2}$, de onde obtemos a forma definida anteriormente.
E como encontramos esses percentis?
Suponha agora que, ao invés de $\gamma = 95\%$, queiramos construir um IC de $\gamma = 90\%$ de confiança.
Como podemos encontrar $Z_{(1 + \gamma)/2}$ nesse caso?
- Alternativa 1: utilizar uma tabela com a CDF da distribuição Normal padrão.
- Alternativa 2: utilizar a função
stats.norm.ppf!
A função stats.norm.ppf toma um argumento p (uma probabilidade, e logo entre 0 e 1) e retorna o percentil equivalente ao valor de p.
#In:
stats.norm.ppf(0.9773)
2.000929388101571
#In:
stats.norm.ppf(1 - 0.9773)
-2.000929388101571
#In:
stats.norm.ppf(0.975)
1.959963984540054
#In:
stats.norm.ppf(1 - 0.975)
-1.959963984540054
#In:
round(stats.norm.ppf(0.975), 2)
1.96
#In:
estimate_z()
HBox(children=(FloatSlider(value=2.0, description='z', max=4.0, step=0.05),))
Output()
Dessa forma, se quisermos construir um IC90% para a média populacional, primeiramente calculamos os percentis 5% e 95%:
#In:
stats.norm.ppf(0.05)
-1.6448536269514729
#In:
stats.norm.ppf(0.95)
1.6448536269514722
Depois, basta substituir na fórmula que tínhamos anteriormente:
#In:
left_normal = sample_mean_mean - 1.64 * sample_mean_sd
right_normal = sample_mean_mean + 1.64 * sample_mean_sd
[left_normal, right_normal]
[10.956177214345448, 15.05982278565455]
#In:
## for more precision (and efficiency), we can simply call
left_normal = sample_mean_mean - stats.norm.ppf(0.95) * sample_mean_sd
right_normal = sample_mean_mean + stats.norm.ppf(0.95) * sample_mean_sd
[left_normal, right_normal]
[10.95010478606978, 15.065895213930219]
Resumo: Bootstrap vs. TCL
| Bootstrap | TCL | |
|---|---|---|
| Prós | Funciona para várias estatísticas diferentes (média, mediana, desvio padrão). | Precisa de apenas 3 quantidades – média amostral, DP amostral e tamanho amostral. |
| Contras | Computacionalmente intensivo (requer a simulação de muitas e muitas amostras da amostra original). | Funciona apenas para a média/soma amostral. |
Teste rápido ✅
Qual desses histogramas corresponde à distribuição da média amostral para amostras de tamanho $n = 100$ tiradas de uma população com média $\mu = 50$ e DP $\sigma = 20$??
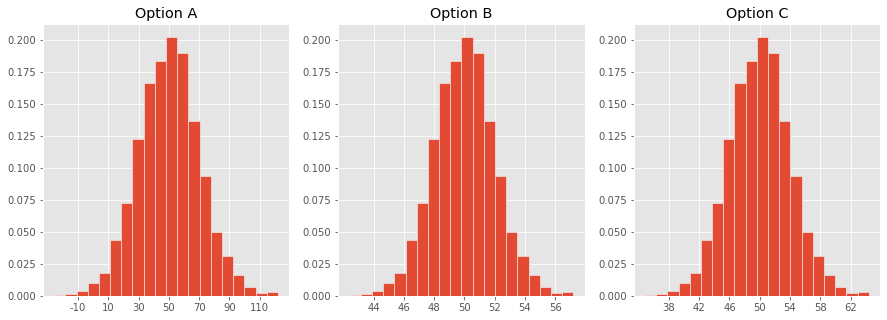
Resumo e próxima aula
Resumo
- O Teorema Central do Limite nos diz que a distribuição de probabilidade da média amostral de uma amostra com tamanho suficientemente grande será aproximadamente Normal, qualquer que seja a população original da qual a amostra é coletada.
- Esse resultado também vale para diversos tipos de somas.
- O TCL também nos diz que:
- A distribuição da média amostral será centrada na média populacional;
- O DP da distribuição da média amostral é igual a $\sigma/\sqrt{n}$.
- Com base no TCL, podemos construir um IC de $\gamma\%$ de confiança para a média populacional $\mu$ da seguinte forma:
\begin{equation} IC_{\gamma\%}(\mu) := \bar{X} \pm Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}} = \left[\bar{X} - Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}}; \,\,\,\, \bar{X} + Z_{(1 + \gamma)/2} \cdot \frac{S}{\sqrt{n}}\right], \end{equation}
em que $Z_{(1 + \gamma)/2}$ denota o percentil $(1 + \gamma)/2$ da distribuição Normal padrão.
Próxima aula
- Discutiremos como escolher tamanhos de amostra com base na precisão desejada para nossas estatísticas0.
- Por exemplo, se quisermos construir um IC com amplitude de no máximo $w$, qual o tamanho de amostra necessário para isso?
- Introduziremos noções básicas de como testar hipóteses acerca da população da qual amostramos.